I have a challenge and small prize associated with breaking ISAAC.

The files below implement ISAAC in C. The function randinit() must be called before ISAAC can be used, but after that any module that #includes rand.h can call rand() to get 32-bit random values.

• standard.h
• rand.h
• rand.c (rand.c is optimized for speed)
• randport.c (randport.c is optimized for speed except it's portable to platforms where integers are bigger than 4 bytes or characters are bigger than 1 byte)
• readable.c (readable.c produces the same results as rand.c but the C code is easier to read, and it doesn't need rand.h or standard.h)
• randvect.txt (the results if you compile any of these with -DNEVER and run it)
• randseed.txt (the results if you do "gcc -O rand.c randtest.c -o rand" then run rand)

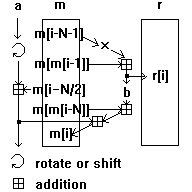
ISAAC (Indirection, Shift, Accumulate, Add, and Count) generates 32-bit random numbers. Averaged out, it requires 18.75 machine cycles to generate each 32-bit value. Cycles are guaranteed to be at least 2⁴⁰ values long, and they are 2⁸²⁹⁵ values long on average. The results are uniformly distributed, unbiased, and unpredictable unless you know the seed.

Others have translated ISAAC into other languages:

• Pierre Abbat has implemented ISAAC in Forth (local copy).
• Quinn Tyler Jackson translated it to C++.
• Greg Vigneault has implemented it in Modula-2, a language that doesn't support bit operations! (local copy)
• Sebastian Sauvage translated it into Delphi (local copy).
• John L. Allen translated it into Perl.
• Daniel Berlin produced a Java implementation that I haven't got around to checking yet.
• Marv Schwartz translated Isaac into C#.
• I translated it into Java, as well. It had a bug for a long time that made it initialize differently than the C version, but Paul Wankadia pointed it out and I fixed it (Sept 30 2005).
• Kenneth Ives translated it into Visual Basic, with tests.
• Doug Hoyte translated it into Haskell (local copy).
• Doug Hoyte translated it into Lisp, too (local copy).
• Gerald Moull has translated it into Cobol.
• Wolfgang Ehrhardt has implemented it in Pascal, along with many other PRNGs.
• Ilmari Karonen translated it into PHP.
• Yves-Marie K. Rinquin implemented it in JavaScript (MIT license)

ISAAC-64 generates a different sequence than ISAAC, but it uses the same principles. It uses 64-bit arithmetic. It generates a 64-bit result every 19 instructions. All cycles are at least 2⁷² values, and the average cycle length is 2¹⁶⁵⁸³.

The following files implement ISAAC-64. The constants were tuned for a 64-bit machine, and a complement was thrown in so that all-zero states become nonzero faster.

• standard.h
• isaac64.h
• isaac64.c

There are lots of random number generators out there. Why use ISAAC?

• Why not use x=ax+b mod p? Because multiplication and mod are slow. On a Sparc it was clocked at being five times slower than ISAAC. Also, ISAAC gives any 32-bit number, while ax+b mod p gives numbers between 0 and p-1 for some prime p. Also, ax+b has easily detected patterns (for example, x_i+1 is always ax_i+b mod p).
• Why not use RC4? RC4 is three times slower, more biased, has a shorter minimum and average cycle length, and is proprietary. No way is known to break either RC4 or ISAAC; both are immune to Gaussian elimination. Use the gap test on scaled-down RC4 to see its bias. (RC4 is still very good, much much better than x=(ax+b)%p.)
• I've written some tests for random number generators, which can be used to test ISAAC, RC4, ax+b mod p, or any random number generator you feel like writing.
• ISAAC should work on any 32-bit platform. (Porting it to a 64-bit machine like ALPHA may require masking out overflows in a, randrsl, and mm, or it may just need an adjustment of the definition of ub4, or it may work without modification. If someone ports it to an ALPHA, send me mail at bob_jenkins@burtleburtle.net showing me what you did.) The code in isaac64.c has been run on an ALPHA and a x486 with gcc; it produces the same results on both.
• I presented a paper, ISAAC, at the 3rd Fast Software Encryption Workshop. An online version, somewhat more complete than the published version, is here.
• Bias is detectable after 2³⁷ values for RANDSIZL=3, 2⁴⁵ for 4, 2⁵³ for 5, 2⁶¹ for 6, 2⁶⁹ for 7, and 2⁷⁷ values for RANDSIZL=8.
• Challenge, started 1996/march/27: The files
  • standard.h
  • rand.h
  • rand.c
  • randtest.c
  randtest.c gives the first 2560 results of ISAAC initialized with an unknown seed, along with the program that initialized ISAAC and produced the results. What was the seed? Send mail to bob_jenkins@burtleburtle.net. (Converting bytes to ub4's is endian-dependent, so the seed will only be English on something like an 80?86 machine.)

  I changed the seed 1998/february/10 because I can't reproduce the old seed. Breaking either the old or the new counts.

• PRIZE, started 1998/february/6: $1000 (USA dollars) to whoever sends me the solution to the above challenge (plus publicly revealing a repeatable method for determining it) first. I'll also offer $100 for the first bias that can be detected with RANDSIZL=8 (in sequences of length less than 2⁶⁴ values) (starting with almost all seeds) (exceeding an absolute value of 4 times the standard deviation) (the test must start not knowing the seed).

  ISAAC hasn't been broken since it was published 11 years ago. No bias has been detected either. I am offering these prizes in an attempt to get others to try to break it and assure those techniques are published. Apologies for having such a small prize. If you find successful attacks or biases in smaller versions of ISAAC, I'll include them in isaac.html, even though there are no prizes for them. I'm interested in attacks and biases against RC4 as well. Other fast stream ciphers are SEAL and WAKE.

Attacks on ISAAC by someone other than Bob Jenkins:

• 2001: Marina Pudovkina published an attack on ISAAC with estimated running time of 4.67x10¹²⁴⁰.
• 2006: Jean-Phillipe Aumasson pointed out that I provided no official way of seeding ISAAC. If the lack of an official seeding routine is interpreted as allowing a null seeding routine (directly setting the internal state to a known value), that allows the output to be predicted.

  I provided no official seeding routine because I didn't feel competent to give one. Seeding a random number generator is essentially the same problem as encrypting the seed with a block cipher. ISAAC should be initialized with the encryption of the seed by some secure cipher. I've provided a seeding routine in my implementations, which nobody has broken so far, but I have less faith in that initialization routine than I have in ISAAC.

  As ISAAC is intended to be a secure cipher, if you want to reseed it, one way is to use some other cipher to seed some initial version of ISAAC, then use ISAAC's output as a seed for other instances of ISAAC whenever they need to be reseeded.

Internal links:
Hash functions and block ciphers
Perpetual motion machines
Table of Contents