A sequence of new pseudorandom number generators are developed: IA, IBAA, and ISAAC. No efficient method is known for deducing their internal states. ISAAC requires an amortized 18.75 instructions to produce a 32-bit value. There are no cycles in ISAAC shorter than 240 values. The expected cycle length is 28295 values. Tests show that scaled-down versions of IBAA are unbiased for their entire cycle length. The alleged RC4 is used for comparison. No proofs of security are given.
The sections of this paper are Abstract, Introduction, RC4, IA, IBAA, Tests, ISAAC, and Summary.
The purpose of this paper is to introduce the new random number generators IA, IBAA, and ISAAC. IA (Indirection, Addition) is biased but it appears to be secure. It is immune to Gaussian elimination. IBAA (Indirection, Barrelshift, Accumulate and Add) eliminates the bias in IA without damaging security. ISAAC (Indirection, Shift, Accumulate, Add, and Count) is faster than IBAA, guarantees no bad seeds or short cycles, and makes orderly states disorderly faster. The generator for RC4 will be used for comparison throughout this paper.
IA was designed to satisfy these goals:
More requirements were added for IBAA:
ISAAC took away the requirement of easy memorization but added more:
ISAAC-64, a version for 64-bit machines which requires 19 instructions to produce a 64-bit result, is implemented in standard.h, isaac64.h, and isaac64.c. The constants were tuned for 64-bit arithmetic using the avalanche test, and a complement operator was thrown in to mix all-zero states.
Notation: we will use ^ to represent exclusive-or. ALPHA is the log of the number of bits in an array; looking up a value in an array requires an offset of ALPHA bits. SIZE is 2ALPHA, the size of the array.
An alleged implementation of RC4 (Ron's Code \#4) was posted September
13, 1994 anonymously on the Internet newsgroup sci.crypt \cite{rc4}
without permission or verification from
Ron Rivest. It
contained an initialization routine, which we will ignore, and a
random number generator.
(
Here is a collection of RC4 analysis on the web.) The code for the
random number generator will produce the same sequences as
the
generator posted to sci.crypt. We will refer to it as RC4. The
internal state contains a 256-term array (m) filled with a
permutation of the values 0..255, and an accumulator
(a) which holds a value in 0..255. The
initialization guarantees that originally a != i, which
avoids a class of short cycles that plague this generator.
C code for generator for RC4 /* * SIZE is (1<<ALPHA) = (1 times 2 to the 8th) = 256. * ind(x) is the low order 8 bits of x, or x mod 256. */ #define ALPHA (8) #define SIZE (1<<ALPHA) #define ind(x) (x&(SIZE-1)) static void rc4(m,r,aa) int *m; /* Memory: array of SIZE ALPHA-bit terms */ int *r; /* Results: the sequence, same size as m */ int *aa; /* Accumulator: a single value */ { register int a,x,y,i; a=*aa; for (i=0; i<SIZE; ++i) { x=m[i]; a=ind(a+x); y=m[a]; m[i]=y; m[a]=x; r[i] = m[ind(x+y)]; } *aa=a; }
The random values in r are selected from the array
m, and two elements of m are swapped for every byte
reported. The security stems from the difficulty of knowing where any
value is in m, and from the difficulty of knowing which
locations in m are used in selecting each value in the sequence.
The swap of a known position with an unknown position thwarts Gaussian elimination. Gauss can only be applied when we know that a value is used in two equations. Since every swap might change any value, we never know when a position's value changes, so there is no way to be sure that one equation is using the same value as another.
There are almost-detectable biases in the results of RC4 (see the
tests). There are also windows into
RC4's internal state. The relationship
r[i]+x=i occurs 1/256 too often (twice as often as
expected), as does r[i]+y=a. These windows only allow the
position of values to be known with probability 1/128 rather than
1/256; they are not enough to deduce the internal state.
The states with m[i]=1 and
a=i all lie on short cycles. There are 254! short cycles of
65280 values apiece. RC4 is initialized so that they are never hit.
1/65536 of all internal states are on one of these short cycles. The
fact that they are never hit gives an almost-noticeable bias to RC4.
For every sequence that can be produced by RC4, there are 256 internal states that produce the same sequence of ind(x+y). If (m[0..255]=m_0..m_255,a,i) are one such state, then (m[0..255]=m_n..m_((n+255) mod 256), (a-n) mod 256, (i-n) mod 256) is another such state. (These equivalent states were first noted by Paul Crowley on sci.crypt.) Although ind(x+y) is the same for each such sequence, m[ind(x+y)] (the reported result) will be different for each such sequence. The 256 such sequences will have the same length. A single cycle may contain 1, 2, 4, 8, 16, 32, 64, 128, or 256 such equivalent sequences, in which case there will be 256, 128, 64, 32, 16, 8, 4, 2, or 1 such cycles. For example, the short cycles mentioned earlier pass through a sequence of 255 values before mapping to an equivalent of the starting state -- all 256 equivalents of the starting state are on one cycle, so each short cycle is 255*256 values long.
Smaller versions of RC4 can be made by reducing the array size and
the number of bits per value in the array. If the array size is
2ALPHA, then each value should have ALPHA bits.
The new generator IA was designed to be secure, fast and easy to memorize. C code for IA is given below.
C code for IA typedef unsigned int u4; /* unsigned four bytes, 32 bits */ #define ALPHA (8) #define SIZE (1<<ALPHA) #define ind(x) (x&(SIZE-1)) static void ia(m,r,bb) u4 *m; /* Memory: array of SIZE ALPHA-bit terms */ u4 *r; /* Results: the sequence, same size as m */ u4 *bb; /* the previous result */ { register u4 b,x,y,i; b = *bb; for (i=0; i<SIZE; ++i) { x = m[i]; m[i] = y = m[ind(x)] + b; /* set m */ r[i] = b = m[ind(y>>ALPHA)] + x; /* set r */ } *bb = b; }
Like RC4, IA operates on a secret array
m of 256 values. Unlike RC4, the values in m should
contain at least 2ALPHA bits. Like RC4, IA uses pseudorandom
indirection to determine its results. Unlike RC4, the results given
by IA are the sum of values in m, not actual values in it.
Also unlike RC4, IA does not swap values in m, instead it
walks through the array adding pseudorandomly chosen terms to the old
terms.
IA, like RC4, is reversible: every internal state has exactly one
predecessor. The average cycle length of all elements in all reversible
mappings of s states is about s/2, while the average cycle length
of all elements in all irreversible mappings is about
\sqrt{s} \cite {kolchin}
\cite{odl}. In addition to having every
internal state on some cycle, reversible generators tend to have over
half the states on the same cycle (see the test
results), giving the sequences a very uniform distribution.
Notice in IA that when x is added
into r[i]=b, x is no longer in m.
Therefore x came from a different pool of values than the
pseudorandom term that is added in with it. If this were not the
case, IA would not be reversible and the results would be biased in
favor of even values.
The two indirections bracket the user's result. r[i] is the old
value of m[i], but with a pseudorandomly chosen value added.
The new value of m[i] is the user's previous result, but with a
different pseudorandomly chosen value added. There is no equation
which does not contain a new pseudorandomly chosen value. If the
pseudorandom values are treated as unknowns, this is enough to thwart
Gaussian elimination. Guessing what the choice was means guessing 8
bits of information per value.
There are windows into the internal state of IA.
The relationship ind(m[i])=ind(r[i]-i)
is 1/256 too probable, as is
ind(m[i-SIZE]>>8)=ind((r[i]>>8)-i). They happen when a
pseudorandom indirection chooses itself. Each relationship holds
1/128 of the time.
It is possible to avoid these windows by limiting each
pseudorandom choice to the half of the array which does not include
the value used for the pseudorandom choice (x or y).
This would leave only 128 values for each pseudorandom choice, giving
256 relationships that are correct 1/128 of the time (as opposed to
the two relationships we have now). The proposed modification also
makes the code slower, more complicated, and more biased, so it was
not done.
Biases can be detected in IA using the correlated gap test. These biases are similar in nature to those seen in lagged-Fibonacci and add-with-carry generators \cite{ADDNCARRY}. The biases are smaller than the previously noted windows into the internal state.
No efficient attack is known against either RC4 or IA. A brute force attack was written which breaks RC4
with ALPHA=4 in two to ten minutes. The guess-and-generate attack, which applies the equations
of IA to an arbitrary initial guess but sets b to the real
results of IA, converges to the true state of IA after about 213
values when ALPHA=3. Neither attack can be extended to the
next ALPHA, let alone ALPHA=8.
2001: Marina Pudovkina published an attack on ISAAC with estimated running time of 4.67x101240. If you guess all the indirections you can use Gaussian elimination to derive the internal state.
(Guessing all the indirections up front is overkill. I speculate that if you guess a few bits, derive what you can, guess a few more bits, and so forth, you could break it in about 700 guessed bits (the same as brute-forcing 2700 keys). I base that on experience with this attack on RC4; I haven't tried it on ISAAC or IBAA.)
2006: Souradyuti Paul and Bart Preneel proposed a very efficient distinguishing attack on ISAAC in Asiacrypt 2006. Jean-Phillipe Aumasson reports that they got the ISAAC algorithm wrong, so they were attacking the wrong thing, so this attack was irrelevant.
2006: Jean-Phillipe Aumasson posted a distinguishing attack that requires 248 results. However, the claimed bias does not exist. He predicted this bias based on sets of weak states. The bias does exist if results are measured from just those states. The overall bias does not exist because the remaining states have a complementary bias. It is not possible to tell from just the results whether or not the generator is in one of the weak states he defines.
Specifically, Jean defined W1 as the 2-32 fraction of states where m[0]=m[1]. For 254/65536 of these states, r[0]=m[0]+m[j] and r[1]=m[0]+m[j] and j in 2..255, so r[0]=r[1]. Assuming the remaining states are uniformly distributed, r[0]=r[1] with probability about 2-32(1+254/65536). Well, now define V1 as the 254/65536 fraction of states where r[0]=m[0]+m[j] and r[1]=m[1]+m[j] for j in 2..254. For the 2-32 fraction of states in V1 where m[0]=m[1], r[0]=r[1]. Those are the states that lead to the bias in W1. However, for all the remaining states in V1, m[0]!=m[1], so r[0]!=r[1]. The total probability of r[0]=r[1] in V1 is 2-32, exactly what it should be. The same arguments go for r[0]=m[0]+m[1], r[1]=m[1]+m[j], m[0]=m[j], j in 2..255.
However, if you had prior knowledge of the internal state (for example because it was seeded directly with no mixing, with a known pattern) then you might know you were in one of Jean's states. ISAAC does require an initialization routine when the set of keys is smaller than the set of all possible states, or is not uniformly distributed. My default initialization routine is randinit() in rand.c. I haven't discussed randinit(), I have less faith in it than in ISAAC. In this paper, I've only discussed ISAAC once properly initialized, not how to properly initialize it. It's properly initialized if nothing is known about its internal state.
Proving the security of IA or RC4 would require showing that no algorithm could efficiently deduce their internal state. No algorithm examined so far can deduce their internal states, and Gaussian elimination is one of the algorithms that has been examined. This is not a proof by any means, but it is a start.

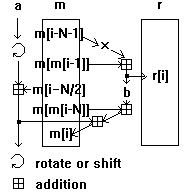
The diagram shows how IBAA or ISAAC produces one result in r[] and replaces one term in m[].
IA was extended to IBAA. In addition to being fast, easy to memorize, and immune to Gaussian elimination, IBAA was required to have no detectable bias for the entire cycle length. Short cycles must be very rare. C code for IBAA is given below. The next section gives the results of statistical tests on IBAA; it does seem to be unbiased.
C code for IBAA /* * ^ means XOR, & means bitwise AND, a<<b means shift a by b. * barrel(a) shifts a 19 bits to the left, and bits wrap around * ind(x) is (x AND 255), or (x mod 256) */ typedef unsigned int u4; /* unsigned four bytes, 32 bits */ #define ALPHA (8) #define SIZE (1<<ALPHA) #define ind(x) ((x)&(SIZE-1)) #define barrel(a) (((a)<<19)^((a)>>13)) /* beta=32,shift=19 */ static void ibaa(m,r,aa,bb) u4 *m; /* Memory: array of SIZE ALPHA-bit terms */ u4 *r; /* Results: the sequence, same size as m */ u4 *aa; /* Accumulator: a single value */ u4 *bb; /* the previous result */ { register u4 a,b,x,y,i; a = *aa; b = *bb; for (i=0; i<SIZE; ++i) { x = m[i]; a = barrel(a) + m[ind(i+(SIZE/2))]; /* set a */ m[i] = y = m[ind(x)] + a + b; /* set m */ r[i] = b = m[ind(y>>ALPHA)] + x; /* set r */ } *bb = b; *aa = a; }
The lack of bias in IBAA comes from the accumulator a.
The term added to a is m[ind(i+(SIZE/2))]. Why were
x or y not used instead, seeing how they are already in
registers? This decision was made based on a single series of tests.
(See the testing section for more detailed descriptions of the terms
and methods here, or chi.c for a testing tool.)
The tests were on IBAA, except m[ind(x)] and
m[ind(y>>ALPHA)] were replaced with 0 and
0. The generator was scaled down to have 8 terms (not 256) of
3 bits apiece (not 32). With a total of 30 bits of state, it had a
maximum cycle length of 230 calls.
ind(i+(SIZE/2)) was replaced with ind(i+j), for each
j \in 0..7. Each of these eight generators produced a
sequence of 227 calls, or 230 values. No
cycles were detected. The low-order bit was removed from each value,
leaving sequences of 2-bit values. The gap test was applied to each
of these sequences, tracking gaps of length 0..63. The expected
\chi2 result was 63, but the actual results (ordered by
j) were 684, 412, 208, 201, 212, 203, 682, and 13584. The
difference from 63 is proportional to the amount of bias detected. In
all cases the first bad gap was of length 10. No other tests detected
significant amounts of bias, so the decision had to be based on this
alone. It appears that the bias decreases with the distance from
either endpoint, so m[ind(i+(SIZE/2))] was chosen.
barrel(a) is a permutation of a, and is nonlinear when
combined with addition. Permutations help assure that all values are
equally likely. Nonlinear systems are less prone than linear systems
to mixing values then spontaneously unmixing them after they have
been churned for awhile. The security of IBAA, however, does not
depend upon this nonlinearity. The security depends upon the
indirections m[ind(x)] and m[ind(y>>ALPHA)].
If m[i], m[ind(x)] and m[ind(y>>ALPHA)]
are treated as separate unknowns, then every set of equations has at least
4/3 as many unknowns as equations.
Let a set of 3n equations (n setting a,
n setting m, and n setting r) be
given. It will produce at least 4n unknowns: n each
of a, m[i], m[ind(x)], and
m[ind(y>>ALPHA)]. Eliminating any subset of these
equations only increases the ratio of unknowns to equations. A more
detailed analysis can be found here.
If an arbitrary reversible mapping has N possible values, then the
chance of an arbitrary starting point being on a cycle of length N/x
or less is 1/x. The number of internal states of IBAA is 28264,
so the chances of arbitrarily choosing a cycle shorter than 240
are about 2-8224.
About 2420 protons could
fit in the known universe \cite{Pound}. The state of all zeros forms
a cycle of length 256 though; after i passes through 0..255
the state maps back to all zeros.
C code for these tests is in chi.c, and other test suites can be found here.
Tests run against random number generators with 256-term internal states often will not fail no matter how long they are run. The cycle lengths of such random number generators are more than astronomical. In order for statistical tests to be of use, generators need to be scaled down. The number of terms in the array and the size of the terms must be reduced. This has a number of advantages.
The tests run were Knuth's frequency, gap, and run tests \cite{Knuth}. The frequency test counts how many times each value appears. The gap test measures the gaps between occurances of values in the results. For example, the sequence "abcdeaf" has a gap of 4 between occurances of "a". The gap test measured gaps up to four times the length of the internal array. The run test counts the lengths of strictly increasing subsequences. The expected distribution of values for a truly random sequence is known for each of these tests, and was compared against the sample distributions using the standard \chi2 formula \cite{Knuth}.
Two types of values were used, "normal" and "correlated". Random number generators are designed to produce lots of random values. These are the "normal" values. "Correlated" values were derived from groups of normal values. There is one correlated value per call to the generator; it has as many bits as the normal values but is composed of the low-order bit of the first few normal values. Correlated values could identify patterns that occurred between calls.
The initial seed in all cases was m[i]=i, a=1, b=1. Each
generator was warmed up by making ten calls before statistics were
gathered.
ALPHA (a) is the log of the length of m,
BETA (b) is the number of bits in
each value, and SHIFT (s) is the amount of the
barrelshift (relevant only to IBAA).
The normal values are either the whole values in r or the low-order
ALPHA bits of each r value.
In the scaled-down versions of IBAA, SHIFT was chosen to be the integer
closest to the golden ratio (.618) times BETA \cite{Knuth5}.
These shift values seem to work well. No reason is known for why
they should work well. The scaled-down versions still are not quite
IBAA, because the values usually had fewer than 2ALPHA bits.
Many bits of ind(y>>ALPHA) were always zero, so the
pseudorandom choices were very restricted.
Test results are given below. If a test would have taken more than a day to run and tests on smaller generators had failed to detect any bias, then the test was not run.
Test results for RC4 and IBAA RC4 correlated normal correlated normal normal number frequency frequency gap gap run of calls ------ ---------- --------- ---------- --------- ------ -------- a1b1 1:0 1:0 7:2 7:22 1:0 3 a2b2 3:4 3:0 15:10 15:11 3:25 49 a3b3 7:33 7:1 31:20 31:280 7:10 119437 a4b4 15:21 15:24 63:85 63:128 7:3 2^^20 a5b5 31:39 31:29 127:132 127:185 7:9 2^^23 a6b6 63:61 63:62 255:228 255:246 7:3 2^^26 a8b8 255:270 255:256 1023:956 1023:1044 7:14 2^^26 IBAA correlated normal correlated normal normal number frequency frequency gap gap run of calls ------ ---------- --------- ---------- --------- ------ -------- a1b1s1 1:0 1:0 7:4 7:13 1:2 5 a1b2s1 3:2 3:1 7:4 7:3 3:0 12 a1b3s2 3:0 3:0 7:5 7:11 3:7 3164 a1b4s2 3:3 3:6 7:6 7:3 3:0 10441 a1b5s3 3:0 3:0 7:14 7:5 3:6 235491 a1b6s4 3:5 3:7 7:5 7:2 3:3 1869951 a1b7s4 3:0 3:0 7:1 7:7 3:0 221862935 a2b2s1 3:0 3:1 15:7 15:11 3:1 1407 a2b3s2 7:6 7:7 15:21 15:8 7:3 29382 a2b4s2 15:9 15:11 15:16 15:7 7:9 6146999 a2b5s3 15:12 15:12 15:15 15:12 7:7 9507107 a3b3s2 7:3 7:0 31:44 31:49 7:5 886828921 a8b32s19 255:238 255:215 1023:949 1023:1016 7:5 2^^26 A result 15:9 means expected 15, actually got 9. A test is said to pass if the actual result differs from the expected result by less than four times the square root of the expected result. The normal gap test failed for RC4 a1b1, a3b3, a4b4, and a5b5, and was questionable for IBAA a3b3s2. The normal run test failed for RC4 a2b2. The number of calls was the cycle length or some round number. The cycle length for IBAA a2b5s3 was unusually short.
Further tests were run later, in 1998, after computers and compilers made longer tests practical. For fullscale RC4, run for 231 calls (239 values) the gap test showed
gap: expect 7 get 43.2641 0.999980 1.000025 1.000055 0.999918 1.000035 0.999945 1.000074 1.000000Paul Crowley's separate tests suggest the first gap should have positive bias (not negative) so random fluctuations are that big in this test. Gaps of length 3 and 4 show noticable problems.
ISAAC, with RANDSIZL scaled down to 3 (but still 32 bit values), also had bias at 237 calls (240 values). Its gap test results for the bottom 3 bits of each value were:
gap: expect 31 get 145.7432 1.000001 1.000002 0.999995 1.000004 1.000000 1.000012 1.000001 1.000000 1.000010 1.000022 0.999989 0.999997 0.999991 0.999979 0.999991 0.999964 0.999984 0.999983 0.999988 0.999988 0.999982 0.999984 1.000012 0.999982 0.999963 1.000014 1.000009 1.000007 1.000003 1.000016 1.000008 1.000043The first 8 gaps only have random fluctuations. Same for the 9th gap, but the 10th and 16th have noticable biases.
Full scale ISAAC, run for 240 values, looking at the bottom 8 bits, had no detectable bias for gaps up to length 1024. Further tests are being run to see how the bias scales. Producing a trillion values takes a week of computer time, so this may take a while.
A common requirement of cryptographically secure random number
generators is that all detectable biases b decrease exponentially
with some polynomial function f of the size s of the internal
state: b < 2-f(s) \cite{BBS} \cite{Yao}. A linear
increase in the number of bits in the internal state should cause all
biases to fall off exponentially. The length of a subsequence
required to detect bias is inversely proportional to the square of the
bias. Both reversible and irreversible generators have expected cycle
lengths that increase exponentially with s, so detecting
excessive bias should be possible when it exists.
RC4 failed the gap test after 215, 219, and 223, and 231 calls with internal states of 27, 68, 165, and 2056 bits respectively. Each internal state is more than double the size of the previous one. This bias seems to be dropping with the square of the number of terms, not exponentially, so RC4 does not satisfy this requirement. IBAA and ISAAC each had bias detected in only one configuration so far, so extrapolation isn't possible yet. They probably don't satisfy the requirement either.
The cycle lengths of IBAA were considerably longer than the cycle lengths for the same-sized version of RC4, mostly because RC4 requires the internal state to be a permutation while IBAA does not. For instance, 3-bit RC4 had a cycle of 119437 calls, while 3-bit IBAA had a cycle length of 886828921 calls.
Tests suggest that all consecutive 256-value strings are equally likely
results from IBAA, 256 being the number of terms in r.
No tests on samples of that size or smaller ever failed, even for IA
which has known biases. The gap and run tests in particular only fail
if they look at subsequences of more than 2ALPHA values
\cite{Knuth}. All 8192-bit strings are equally likely in m;
there are 264 such states for every string (one for each
possible value of a and b). This is not the case
for RC4 because m in RC4 holds a permutation of 0..255,
not a set of arbitrary values. The gap test does fail for
scaled-down versions of RC4 for gaps of length one and two.
It should be noted that these tests were unfair to IBAA. Since
the values usually had fewer than 2ALPHA bits, many bits of
ind(y>>ALPHA) were always zero, so the pseudorandom choices were
very restricted.
George Marsaglia's DIEHARD test suite \cite{DIEHARD} was found shortly before this paper went to print. Two samples each from full-scale IBAA and ISAAC were tested. Although each sample had some test return questionable results, no test had questionable results for both samples for either generator. Separate experiments have seen IBAA develop small biases that fade away as sequences grow longer. Bias peaked in subsequences with about 221 values. ISAAC does not seem to have this problem with short term bias.
IBAA was extended to be leaner, faster, meaner, and have no short
cycles at all -- at the expense of being easy to memorize. The result
is ISAAC, shown below. If the initial internal state
is all zero, after ten calls the values of aa, bb, and cc in
hexadecimal will be d4d3f473, 902c0691, and
0000000a.
C code for ISAAC /* * & is bitwise AND, ^ is bitwise XOR, a<<b shifts a by b * ind(mm,x) is bits 2..9 of x, or (floor(x/4) mod 256)*4 * in rngstep barrel(a) was replaced with a^(a<<13) or such */ typedef unsigned int u4; /* unsigned four bytes, 32 bits */ typedef unsigned char u1; /* unsigned one byte, 8 bits */ #define ind(mm,x) (*(u4 *)((u1 *)(mm) + ((x) & (255<<2)))) #define rngstep(mix,a,b,mm,m,m2,r,x) \ { \ x = *m; \ a = (a^(mix)) + *(m2++); \ *(m++) = y = ind(mm,x) + a + b; \ *(r++) = b = ind(mm,y>>8) + x; \ } static void isaac(mm,rr,aa,bb,cc) u4 *mm; /* Memory: array of SIZE ALPHA-bit terms */ u4 *rr; /* Results: the sequence, same size as m */ u4 *aa; /* Accumulator: a single value */ u4 *bb; /* the previous result */ u4 *cc; /* Counter: one ALPHA-bit value */ { register u4 a,b,x,y,*m,*m2,*r,*mend; m=mm; r=rr; a = *aa; b = *bb + (++*cc); for (m = mm, mend = m2 = m+128; m<mend; ) { rngstep( a<<13, a, b, mm, m, m2, r, x); rngstep( a>>6 , a, b, mm, m, m2, r, x); rngstep( a<<2 , a, b, mm, m, m2, r, x); rngstep( a>>16, a, b, mm, m, m2, r, x); } for (m2 = mm; m2<mend; ) { rngstep( a<<13, a, b, mm, m, m2, r, x); rngstep( a>>6 , a, b, mm, m, m2, r, x); rngstep( a<<2 , a, b, mm, m, m2, r, x); rngstep( a>>16, a, b, mm, m, m2, r, x); } *bb = b; *aa = a; }
These are the differences between IBAA and ISAAC.
rngstep() is essentially the inner
loop of IBAA. Repeating it four times (unrolling the loop) reduced
the loop overhead. This does not affect the results.
m[i] with *m++, r[i]
with *r++, and m[i(SIZE/2)] with *m2++ reduced
the cost of looking up terms in predictable array positions. m
is a pointer, * gets the term it points at, and ++ moves
the pointer up one to the next term. This does not affect the results.
a^(a<<13), a^(a>>6),
a^(a<<2), and a^(a>>16). ^ means XOR and
<< and >> are shifts. Each call to
rngstep() does one of these functions. When machines have no
barrelshift instruction, this saves one instruction per
rngstep(). This sequence of functions also cause a
to achieve avalanche \cite{LLOYD} in 12 rngstep()s. That
causes orderly states to become disorderly faster. Perhaps this
affects the overall bias of the generator one way or the other; there
is no way to tell. It should be noted that each of these functions is
a permutation of a.
cc and i together guarantee a minimum cycle length of
240 values. No cycles are known which are that short. No bad
initial states exist, not even the state of all zeros. Tests have
shown that adding independent things to b does not greatly affect
the generator's bias or security.
y. (IBAA used 0..7 and 8..15.)
This shaved another instruction off each indirect lookup. Scaled-down
tests suggest that the choice of indirection bits does not affect
security or bias, providing no bit is used twice.
All told, ISAAC requires an amortized 18.75 instructions to produce each 32-bit value. (With the same optimizations, IA requires an amortized 12.56 instructions to produce each 32-bit value.) There are no cycles in ISAAC shorter than 240 values. There are no bad initial states. The internal state has 8288 bits, so the expected cycle length is 28287 calls (or 28295 32-bit values). Deducing the internal state appears to be intractable, and the results of ISAAC are unbiased and uniformly distributed. An implementation of ISAAC is standard.h, rand.h, and rand.c.
A sequence of new pseudorandom number generators were developed: IA, IBAA, and ISAAC. Their speed and lack of bias should make them useful for simulations and cryptography. The reader is invited to prove their security (or lack thereof).
Many thanks to the inventor of RC4 and whoever revealed the alleged RC4 publicly. Thanks go to Hal Finney, who first found the short cycles in RC4, and Paul Crowley, who first noticed its symmetric internal states. Thanks go to Colin Plumb for rephrasing an early version of IBAA, Niels J\/orgen Kruse who found a horrible flaw in a slightly later irreversible version, Bill Chambers for reviewing a preliminary draft and suggesting a way to guarantee cycle lengths, John Kelsey, David Wagner, Peter Boucher, Andrew Roos, and, of course, Manuel Blum for introducing me to cryptography in the first place. All mistakes are my own.
A shortened LaTeX version and bibliography are also available.
Reference implementation of ISAAC and ISAAC-64