Filling space with non-colliding orbits

Filling Space with non-colliding orbits

I also have an applet description, a later page building Dyson swarms, exploring gravitation with Java, and a scale model of the solar system.

Is there a set of orbits that:

Guarantees that satellites do not collide at high speed (always frowned upon)
Keeps neighbors next to neighbors (you can't make maps otherwise, indeed there is no sense of locality)
Allows satellites to fill a 3-dimensional volume (there's all that space there, it would be nice to be able to use it)

Yes, there is such a set of orbits. I'll attempt to describe it.

Start with a circular orbit (the blue circle) of period 1.000 circling the sun (the yellow circle). The applet on the right demonstrates this. Click to Start

Make an elliptical orbit, also of period 1.000, in the same plane as the circular orbit (the red ellipse).
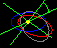These are the same orbits, viewed from an angle, plus a third orbit (the grey ellipse). The grey ellipse also has period 1.000, and is the same shape as the red ellipse, and its major axis is in the same plane as the circular orbit, but the minor axis is tilted out of the plane at about 30 degrees. The green lines try to show the plane of the first two orbits and the angle at which the third is tilted. Click to start

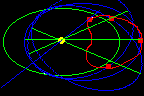The green ellipse is the circular orbit again, and the blue ellipses are copies of the grey orbit. All the blue orbits have period 1.000, their major axes are all in the same plane as the circular orbit (the major axes are the green lines). The red shape is in a plane perpendicular to the circular orbit. The red dots are where the various blue orbits intersect that plane. By taking a single blue orbit and spinning its major axis around the sun in the plane of the circular orbit, a donut-shaped tube is formed, and the cross section of that tube is the red shape. This entire surface can be covered with satellites following blue orbits. Their periods are all 1.000, and neighbors will remain next to neighbors.
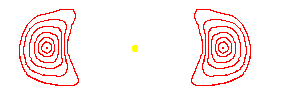The cross-section of the tube is determined by the angle of the minor axis to the circular orbit's plane, and by the eccentricity of the orbits. I don't know exact formulas, but these equations are continuous, and it should be possible to vary these two parameters to form a continuum of donuts, one nested inside the other, with the circular orbit at the very center. All the orbits will have period 1.000, so neighbors will stay next to neighbors. They may get closer and further away at various points in the orbit. The stretching is most amplified in the donuts furthest from the central circular orbit. Click to start. Below is top view. Also, satellites were given significant mass (1/10000 of sun).

Note that if you fill a donut of 3-space with satellites in such orbits, then you can make a map of where the satellites are, and the map does not change over time. The map could be a cylinder standing on one if its circular ends, and any vertical line would represent an orbit. The line down the center would be the center circular orbit.

This all falls apart if the satellites interact, say by having serious mass.

There are several sets of telecommunications satellites in low-earth orbits (GlobalStar, Iridium, GPS, Starlink, ...). Starlink has tens of thousands of satellites in low earth orbit. They actually do follow this, to a degree: the northward half the of the orbit differs in elevation from the southward half by a few miles, guaranteeing no collisions.

How does a globular cluster work? Are collisions very likely? Do stars interact strongly with each other, or do they just orbit the overall center of mass unhindered? Inquiring minds want to know. (It also makes nice pictures.)

Itzu, or Crabs In Space
Why there are no perpetual motion machines
Cryptographic Protocols
Table of Contents

Start with a circular orbit (the blue circle) of period 1.000 circling the sun (the yellow circle). The applet on the right demonstrates this.	Click to Start
Make an elliptical orbit, also of period 1.000, in the same plane as the circular orbit (the red ellipse).
These are the same orbits, viewed from an angle, plus a third orbit (the grey ellipse). The grey ellipse also has period 1.000, and is the same shape as the red ellipse, and its major axis is in the same plane as the circular orbit, but the minor axis is tilted out of the plane at about 30 degrees. The green lines try to show the plane of the first two orbits and the angle at which the third is tilted.	Click to start
The green ellipse is the circular orbit again, and the blue ellipses are copies of the grey orbit. All the blue orbits have period 1.000, their major axes are all in the same plane as the circular orbit (the major axes are the green lines). The red shape is in a plane perpendicular to the circular orbit. The red dots are where the various blue orbits intersect that plane. By taking a single blue orbit and spinning its major axis around the sun in the plane of the circular orbit, a donut-shaped tube is formed, and the cross section of that tube is the red shape. This entire surface can be covered with satellites following blue orbits. Their periods are all 1.000, and neighbors will remain next to neighbors.
The cross-section of the tube is determined by the angle of the minor axis to the circular orbit's plane, and by the eccentricity of the orbits. I don't know exact formulas, but these equations are continuous, and it should be possible to vary these two parameters to form a continuum of donuts, one nested inside the other, with the circular orbit at the very center. All the orbits will have period 1.000, so neighbors will stay next to neighbors. They may get closer and further away at various points in the orbit. The stretching is most amplified in the donuts furthest from the central circular orbit.	Click to start. Below is top view. Also, satellites were given significant mass (1/10000 of sun).