 . Here is another
picture of that balanced orbit from the top after it has precessed all the way
around the sun.
. Here is another
picture of that balanced orbit from the top after it has precessed all the way
around the sun. 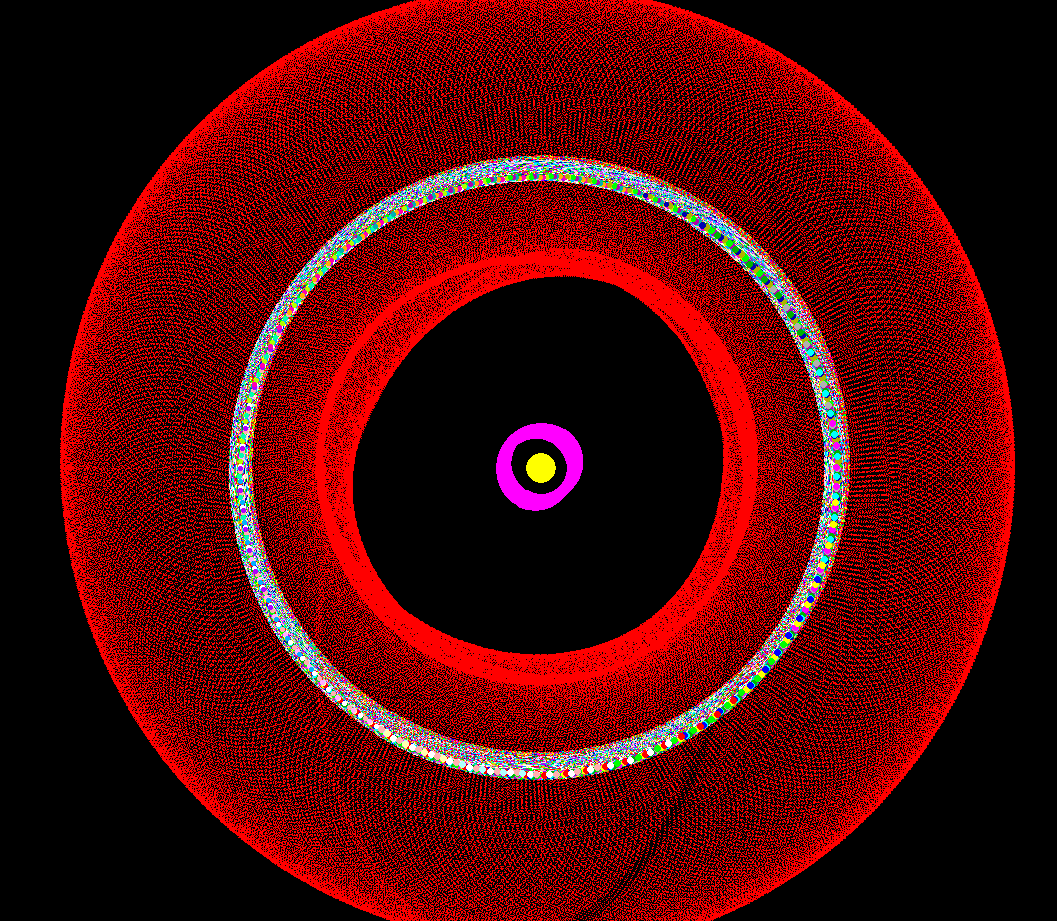 .
.
This describes a Dyson swarm: a set of orbits that capture most or all of the light from a star. This particular design has a surface formed by all the orbits that resembles a doughnut, with the star in the center. We should use it for populating the whole solar system with habitats, and later maybe even other things.
A torus (my definition) is constructed by placing a satellite in an elliptical orbit around a sun and spinning that orbit around some line that intersects the sun and is not in the plane of the ellipse. The structure looks like a glazed doughnut, with flat or concave inner walls. The whole surface of a torus can be covered with satellites with the same period, which do not collide, and where neighbors stay next to neighbors. A continuum of nested nonintersecting toruses can be constructed with these same properties, filling the whole 3d volume of the torus with noncolliding orbits.
SpaceX's starlink swarm is actually one of these, with a big tilt and an extremely small eccentricity: it's centered on the equator but the tilt brings it up to about the Canadian border, and the eccentricity keeps the inner and outer surface just a few miles apart.
Here's my old page on toruses. Below is a simulation in javascript of a torus-style Dyson swarm, as seen from an object in the torus. (I have other pages using the same orbit simulator.)
In 1959, the imaginative Freeman Dyson proposed capturing all the light coming out of a star with a swarm of satellites. He didn't say how to arrange the satellites. This became known as a Dyson sphere. Science fiction writers later replaced the swarm of satellites with a solid shell. The swarm of satellites is a Type I Dyson sphere and the shell is a Type II Dyson sphere. Type II is probably impossible: the gravity of the sun would cause the poles of the sphere to collapse. Type I is quite feasible, though. It is also sometimes called a Dyson swarm. Some orbits have been proposed [1] [2] [3]. I checked, yes, these prior designs have precession issues too, even [3] which has all circular orbits.
Several toruses of different sizes and orientations can be used to construct a very different looking Dyson swarm. Some single toruses are nearly a Dyson swarm all by themselves. Toruses have the disadvantage compared to the original proposal of having direct sunlight for only a fraction of the orbit, and of having two holes so a small fraction of sunlight is not captured. They have the advantage of keeping neighbors next to neighbors, no high velocity near misses, and they allow a large 3d volume to be occupied.
Below is a series of nested toruses with tilt=eccentricity. Toruses .0 through .7 do not intersect. Toruses .8 and .9 do intersect each other and the previous toruses. I speculate that the largest nonintersecting torus would have a tilt of sqrt(1/2), about .7071.
Let's look at those near Dyson-swarms again, but with some thickness to the shells this time. We see that if shells intersect earlier shells, any thickness at all means that there will be satellites colliding. As shells approach the limit (tilt .7), satellites get closer and closer together. It's probably best not to exceed tilt of .6. These leave only a 90-degree cone of light coming from the star, so it would only take two toruses to capture all light.
Other concerns: How do you get rid of heat once you've captured all sunlight? The same mechanism catching all light from the sun blocks the entire sky. How important is line-of-sight between satellites in a swarm? How thick should the shell be? Is there any point in populating the interior of toruses?
I think tilt = .5 and .6, tilt=2*eccentricity looks the most promising for an actual Dyson swarm. Thickness of the torus does not cause collisions. The nearest and furthest point from the sun in a given torus aren't too different. Two nested toruses could capture all light, and the outer torus isn't terribly bigger than the inner one. The outer surface of the inner torus and inner surface of the outer torus could have roughly aligned velocities, making it easier to jump between the two. Or you could have three rings (x y z planes) or four rings (a cube with planed-off corners forms four symmetric rings). Or more rings at assymetric angles. More rings allow individual rings to be thinner and with less tilt.
These toruses are passively stable in the short term (a few orbits), but not in the long term (thousands or orbits). They can be made metastable (they would be stable forever if the original placement was just right and there were no perturbations). They can be made long-term stable by active maintenance (tossing masses back and forth and pulling on tethers). Active maintenance can also keep them stable in the face of small unpredictable perturbations, which you'd get a lot of in a populated Dyson swarm.
Position/velocity maintenance has to be done without throwing away mass. No rocket fuel. Not only can't you get mass back after you've thrown it away, the spread-out exhaust will be a nuisance for other satellites. All satellites want to avoid unexpected collisions, and that's easier when you know where everything is and what it's doing. Gas and dust interfere with that.
Because these are orbits, a velocity pushing a satellite out of the ideal surface will be replaced by a velocity pushing it in towards the center sometime later in the orbit. Since maintenance is done over years not minutes, it's fine to defer maintenance until the velocity to be corrected is a convenient one.
Precessing clockwise or counterclockwise doesn't matter, that just
rotates the torus as a whole. You could cure clockwise precession
with a Mercury or a Jupiter, but what is the point? The far point
precessing up or down from the orbital plane matters though, it
would cause collisions for sure
when the far point is also the furthest point from the orbital plane.
A mass in an inner orbit in the orbital plane causes
the far point of an inclined orbit to precess one way. A mass in an
orbit inside the torus (or outside the torus) in the orbital plane
causes the far point to precess the other way. A combination of the
two can keep the near point of
the inclined orbit on the orbital plane, preventing collisions. No energy
required ever provided everything is perfectly balanced. All masses
within the torus cause the near point to precess the same way, though,
you cannot cure this simply by appropriate spacing of nested toruses.
Here is a simulation of a nearly balanced system:
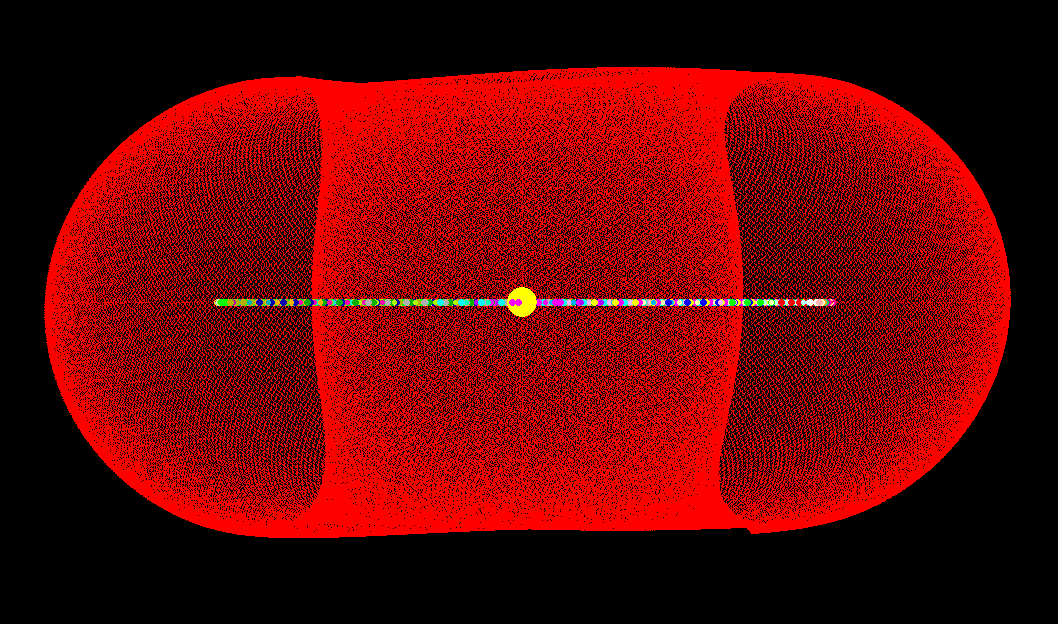
... and since the simulation takes a very long time, here is a screenshot of it
after several hours, showing how the red inclined orbit as it rotated (clockwise?)
all the way around the sun. See, the major axis of the inclined orbit did not migrate
above or below the orbital plane.
 . Here is another
picture of that balanced orbit from the top after it has precessed all the way
around the sun.
. Here is another
picture of that balanced orbit from the top after it has precessed all the way
around the sun.  .
.
Moving along the surface of the torus can be done by pulling on tethers attached to neighbors and throwing rocks to neighbors. As long as you catch as many rocks as you throw on average, mass is conserved. Such adjustments spread out local troubles across the whole torus. If the goal is for everyone to be going the same speed, averaging out always works because there will always be some average.
What to do if the torus's period consistently grows or shrinks? This happens if energy is consistently added to or removed from the orbits. You can radiate energy into space as heat and you can absorb energy from the sun, so you can control total energy bound up in orbits. So, don't allow total energy bound up in the orbits to vary.
OK, actual construction of the continuum of toruses with tilt=eccentricity. Ready? Here goes.
Start with a circular orbit. If the gravitational constant G is 1, and the star has mass 1 at position (0,0,0), and a satellite at position (1,0,0) is travelling at velocity (0,1,0), then that satellite is in a circular orbit of period 2*pi.
Note that the period of a satellite depends on its distance from its star and its absolute velocity, but NOT on its full position or the direction of its velocity. All toruses with period 2*pi are going to be at distance 1 from the star at some point. If I make that the high point of the orbit, the z coordinate of the velocity is conveniently zero. To have tilt=eccentricity, for some tilt d, one spot on that torus is position (sqrt(1-d*d), 0, d), velocity (-d, sqrt(1-d*d),0).
A little trigonometry rotates these starting points about the z axis, for example this program generates these positions and velocities and rotates them about the z axis.
Finally plug all these starting points into an orbit simulator and periodically dump out positions along the resulting orbit to get all the points on the torus that are not exactly distance 1 from the star. (There is a trigonometric way to get those points, but I forget what it is.) If you watch my simulations for awhile, you'll see that the rings quickly diverge. That's because my simulator didn't report the velocity very well. I haven't got around to fixing it.
Now, this construction puts the points with zero z velocity on the sphere of radius 1. The simulator seems to say that that implies that the minimum and maximum distance from the sun will happen at position (?, ?, 0). Why? Also, eyeballing it, it looks like the minimum and maximum distance from the sun are equal distances from the central orbit. Why?
An ellipse can be defined by taking a plane, two points (focii, f1, f2) in the plane, and a length d that is greater than the distance between the two points. A point p in the plane is on the ellipse iff the sum of the lengths of (f1,p) and (p,f2) is d. Orbits are ellipses, with the sun as one of the focii. For the circular orbit, both focii are in the same place and d=2. If you assume all orbits with d=2 have the same period, I can show the rest.
(Ross Millikan pointed out why all orbits with the same d have the same period. d is also the length of the major axis of the ellipse. The "semi-major axis" of an ellipse is half the major axis. Kepler's third law states that the period of an orbit is proportional to the 3/2 power of the length of the semi-major axis. So all orbits with the same d have the same period.)
A point on the minor axis of the ellipse is equidistant from the two focii, and d=2, so it must be distance 1 from both focii. The tangent to that point is horizontal, which explains why the point with zero z velocity is the high point of the torus.
A point on the major axis of an orbit is either the minimum or maximum distance from the sun. The distance to the nearest focus is 1-q (for some q), the sum of the distances to the focii is 2, so the distance to the furthest focus is 1+q. That explains why the minimum and maximum distances from the sun are equidistant from the circular orbit.
An open cluster of 200 suns, from the
perspective of one of the suns
Klemperer rosettes, the solar
system, figure-eight orbits, and all other n-body simulations
Ye Olde Catalogue of Boy Scout Skits
Table of Contents