The problem here is to find a single tile shape with five sides which can tile an infinite floor without leaving holes. I tried finding new solutions, but I think all the tiles I found had been previously found by someone else. Someone claimed the recipe I was using in my search was new.

Here are the known solutions:

• I got started on this because I saw an article in the paper about Marjorie Rice, an amateur mathematician with no training beyond high school, who had discovered the tile used in the background of this page and three others in 1976 and 1977. She used the same search strategy I'm using, but by hand. At any rate, I thought, "I can do that", so I did. (Thanks to H. Nelson Miller for refreshing my memory on the details. Martin Gardner's "Time Travel and Other Mathematical Bewilderments" covers Marjorie Rice.)
• The official list of all pentagons that tile the plane is here. The official definition of a pentagonal tiling is slightly different from mine. Here are a few known solutions.
  
  
• Here are more solutions, boring ones that you get by subdividing more common tiles. (I think these are old, I'm not sure.)
  
  
• Angles 120-60-180-60-120, all sides equal. This is definitely old, but it forms some patterns that no other tile forms. The first pattern shown is a "reptile": 4 tiles form a larger tile of the same shape, and 4 of those form yet a larger tile, and so on recursively. (It's a pentagon because there are five points at which tiles meet. It doesn't matter that the angle at one of the points is 180 degrees.)
  

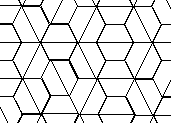
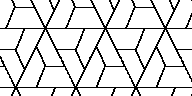
Here are the solutions I found. (I have about 2000 more candidate new solutions, but I haven't developed the tools to judge them. Probably about 6 will be real solutions.)

• Angles 45-270-22.5-112.5-90, four sides equal. This forms only one pattern.
  
• Angles 100-140-60-160-80, all sides equal. The tile and its mirror image are required for this tiling. I just learned the circle is called a "Hisrchhorn Medallion", and was first found by Mike Hirschhorn in the 1970's. I tiled the floor of my half bath with this tiling. Mathematician Ed Pegg, Jr. manufactured a game (sort of like dominoes) out of this tile and another that he found. (I had to get a set to show my support for mathematicians actually building things.)
  
• Angles 108-36-252-36-108, all sides equal. This is easy to derive from a pentagram. It forms many interesting tilings. I've seen it in some of David Eppstein's tilings, so I didn't find it first. I painted it on the ceiling of my half bath.
  
• Angles 60-90-150-30-210, all sides equal. It would be easy to lay floor tiles or linoleum made with this.
  

Here is another solution by Mike Korn:

Here's the recipe I'm using in my search.

David Eppstein's tiling related links
David Eppstein's generally geometric links
Ed Pegg's Chaotic Tiling combines the 160-60-140-100-80 tile with another to produce chaotic tilings.
I decorated my half bath with these tiles.
Here's a gallery of my mom's art.
Table of Contents