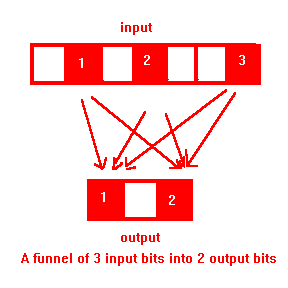
 A hash function is bad if it causes collisions when keys differ in
only a few bits. This always happens when the effects of a number of
input bits are funneled into a smaller number of bits in the internal
state. Funneling formalizes this concept.
A hash function is bad if it causes collisions when keys differ in
only a few bits. This always happens when the effects of a number of
input bits are funneled into a smaller number of bits in the internal
state. Funneling formalizes this concept.
This paper will assume that hash functions are constructed using a standard model. Hash functions have some internal state, and a permutation mix is used to mix this internal state. Another function, combine, is used to combine input blocks with the current internal state.
initialize the internal state;
for (each block of the input)
{
combine (the internal state, the current input block);
mix( the internal state);
}
value = postprocess( the internal state );
return (value);
Although most hashes fit this model,
some (for example MD4 [MD4] and Rogaway's
bucket hash [Rogaway]) do not.
Funneling
Consider the hash function
char hashfun( char *key, int len)
{
char hash;
int i;
for (hash=0, i=0; i<len; ++i) hash=hash^key[i];
return (hash %= 101); /* 101 is prime */
}
(This function requires 5m+3 instructions to hash m
bytes. Compare that to 6m+35 and 5m+41 for the two new
hash functions.)
The keys "ab" and "ba" hash to the same value. The only
difference between the two keys is the first bit of each byte. What
is the problem here? (Ignore commutativity for the moment.)
 A hash function is bad if it causes collisions when keys differ in
only a few bits. This always happens when the effects of a number of
input bits are funneled into a smaller number of bits in the internal
state. Funneling formalizes this concept.
A hash function is bad if it causes collisions when keys differ in
only a few bits. This always happens when the effects of a number of
input bits are funneled into a smaller number of bits in the internal
state. Funneling formalizes this concept.
Let K (keys) be the set of all k-bit values and V (hash values) be the set of all v-bit values. Let a hash function h : K -> V be given. Bits i in 1..k affects bit j in 1..v if two keys differing only at bit i will differ at bit j about half the time, that is between epsilon and 1-epsilon for some epsilon near zero.
Define h to be a funneling hash if there is some subset of t of the input bits which can only affect bits u in the internal state, and |t| > |u| and v > |u|. h has a funnel of those t input bits into those u bits of the internal state. The set of keys differing only in the input bits of the funnel can produce no more than half that number of hash values. (More precisely, if epsilon is zero, those 2|t| keys can produce no more than 2|u| out of 2v hash values.) Keys differing in only a few bits is a common pattern in human and computer keys, so a funneling hash is seriously flawed.
Funneling: there is an efficient test for funnels.
Proof: A set of 2t keys differing in only t bits in a key block will map to 2t distinct values in the internal state after the mapping, and 2t states cannot be represented in less than t bits, so those t original bits will affect t or more bits in the internal state.
Q.E.D. one-to-one
Proof: If there are no funnels yet, the t input bits from previous blocks have affected at least t bits of the internal state. The set of 2t internal states differing in only those t bits will map to 2t distinct internal states after a permutation, and 2t states cannot be represented in less than t bits, so those t original bits will affect t or more bits of the internal state after the permutation.
It may be that those t input bits could cause only (1/(1-epsilon))t variations of those t internal state bits, in which case some compression is possible.
Q.E.D. mix
The proof is the same as for the mixing step.
Q.E.D. combine
When the mixing step is nonlinear, it is very rare that any single
function can cancel out the effects of an already-mixed block, and
even rarer that the combining step is that function.
Let f be the mixing step and + be the combining step.
Let k1 and k2 be text blocks, and
z the internal state of the hash function.
Every (k2, z) fully defines a function
that maps f(k2 +
f(k1 + z)) to
f(k2 + f(0 + z)).
When f is linear this function is always
ff(-k1) + x.
But when f is nonlinear, the mapping can be different for
every k2 and z. This is how nonlinearity
can make it is impossible to cancel the effects of already-mixed
data.
Avalanche
The property of avalanche is that every one of the k input bits changes every one of the v output bits about half the time [Schneier]. Whether a function achieves avalanche can be tested by applying the function about klog(2v) times.
Proof: Assume there were no funnels before the final mixing step. This implies that every input bit has affected at least one bit of the internal state.
If the mixing and postprocessing step together achieve avalanche, then every bit of the internal state before the mix affected every one of the v bits of the result. No input bit affected less than v bits, so no input bit is in a funnel smaller than v bits. By the definition of a funnel, that means there are no funnels at all.
Users do not always use their entire result. If the user only selects q of those v bits, all q of those bits are still affected by every bit of the internal state from before the final mixing step, thus by every input bit.
Q.E.D. postprocess
Users do not always use their entire result. Suppose that for every bit of the internal state there is one input bit from the final block that affected only that bit. If there is a result bit that is not affected by some bit of the internal state, then the user might select only that result bit, and that would be a funnel of 1 bit into 0.
Q.E.D. everybit
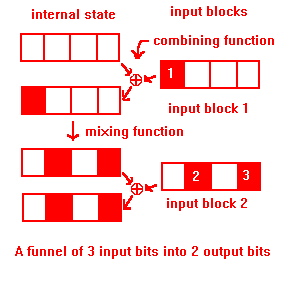
There are a number of cases to consider:
Suppose all the input bits are in one block. Point 1 and lemma Combine shows the funnel does not occur during the combining step, point 2 and lemma Mix during the mixing step, and points 3 and 4 and lemma Postprocess during the postprocessing step. So input bits in one block do not cause funnels.
The combining step will cause every bit in input block k1 to affect at least one bit of the internal state. If the mixing step caused some internal bit to affect only u bits of the internal state, then the next input block k2 will also cause every one of those u bits to be affected by perhaps just one new input bit. This is a total of u+1 input bits affecting u bits of the internal state, which is a funnel if and only if u < v.
Since the mixing step is reversible, it makes sense to ask the same questions in reverse. Affecting v bits forward does not imply that v bits will be affected in reverse. In the mix-combine scheme, if the mixing step does not achieve avalanche in reverse, there will be a bit in k2 that affects only u bits of the internal state (at the time k1 is combined). This is again a funnel of u+1 into u if and only if u < v.
Any two bits affect at least as many bits forward and backwards as any one of those bits (by our definitions of affect and funnel), so the problems with one bit forward and one bit backward are all that need to be considered. If every bit affects at least v bits forward and backward, then there are no funnels with bits spread between adjacent blocks.
There is another case. The problem is with a bit affecting at least v bits by the time the next block is combined, but at some later point in time affecting fewer bits. This requires the mixing function to compress already-mixed data.
Q.E.D. nofunnel